Moving Sofa Problem

The Problem

One of the interesting open math problems emerged in 1966 by Leo Moser. It is described as follows

What is the largest area of a shape that can be maneuvered through a unit-width L-shaped corridor?

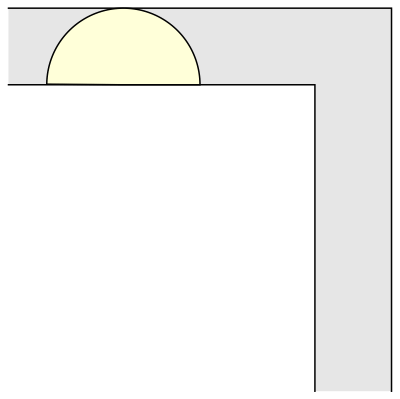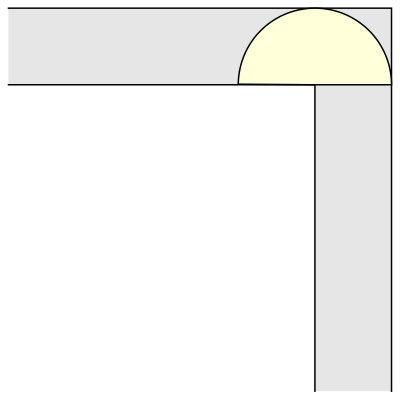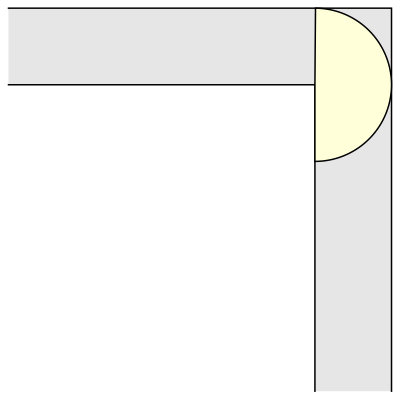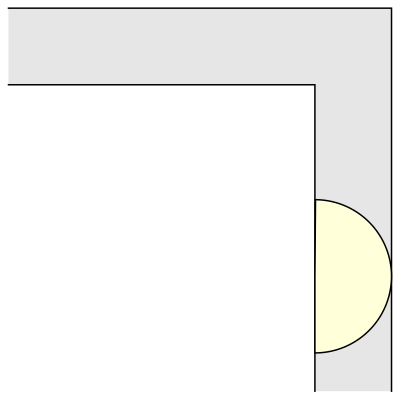
I was introduced to this problem and couldn't get it out of my head

My Approach to Finding the Sofa

I realized this problem could be abstracted to the pivot point of these sofas. If you knew that point then as it translated and rotated around the corridor the extents of the sofa would be defined by the corridor walls themselves

If you could define different continuous paths that included x, y and θ (rotation) you could use that to determine the sofa shape and therefore area

While less rigorous than other mathematical approaches, this intuitive method seemed worth exploring. With this theoretical framework in place, the next step was implementing a practical method to generate and test these paths.

Initial Path Generation

This led to a method of generating paths. It was an interesting first step

After this I changed to using matplotlib to visualize it (faster, more familiar) and were able to also calculate the area using convex hulls.

These developments of the code led to our final product, which gave us some results

.

.

This was the most fun portion of the project -- tweaking parameters and seeing the result was really the output I was hoping for. Feel free to play with it yourself, the code can be found here. Some of the solutions got close to the maximum known answer of 2.2195, but none surpassed it

Presentation

This work happened to coincide with a friend's party where we all gave 10 minute presentation about things we are passionate about. I adapted this project into a brief history of the problem and the work that I did on it. The slides can be found here

Conclusion

This was, at its core, a chance to play with an elegant mathematical puzzle. While not advancing the mathematical bounds of the problem, creating these tools helped me better understand the geometric constraints at play and explore it hands-on. The code and visualizations are available for others who want to experiment with this puzzle