Can You Solve a High Schooler's Favorite Puzzle?

Published on April 5, 2025

The Problem

A teacher is handing out candy to his students, of which there are at least four. He abides by the following rules:

He hands out candy to groups of three students (i.e., "trios") at a time. Each member of the trio gets one piece of candy.

Each unique trio can ask for candy, but that same trio can't come back for seconds. If students in the trio want more candy, they must return as part of a different trio.

When a trio gets candy, the next trio can't contain any students from that previous trio.

It turns out that every possible trio can get a helping of candy. What is the smallest class size for which this is possible?

My Approach to Finding the Answer

Beneath the scenes this is a graph-based problem. Each node represents a possible trio of students, and two nodes are connected by an edge if they don't share any students in common (meaning they can follow each other in the sequence).

By modeling it as such and using a greedy approach for finding a valid traversal that hits all nodes, we are able to find a path that includes all 35 combinations for the 7 student case.

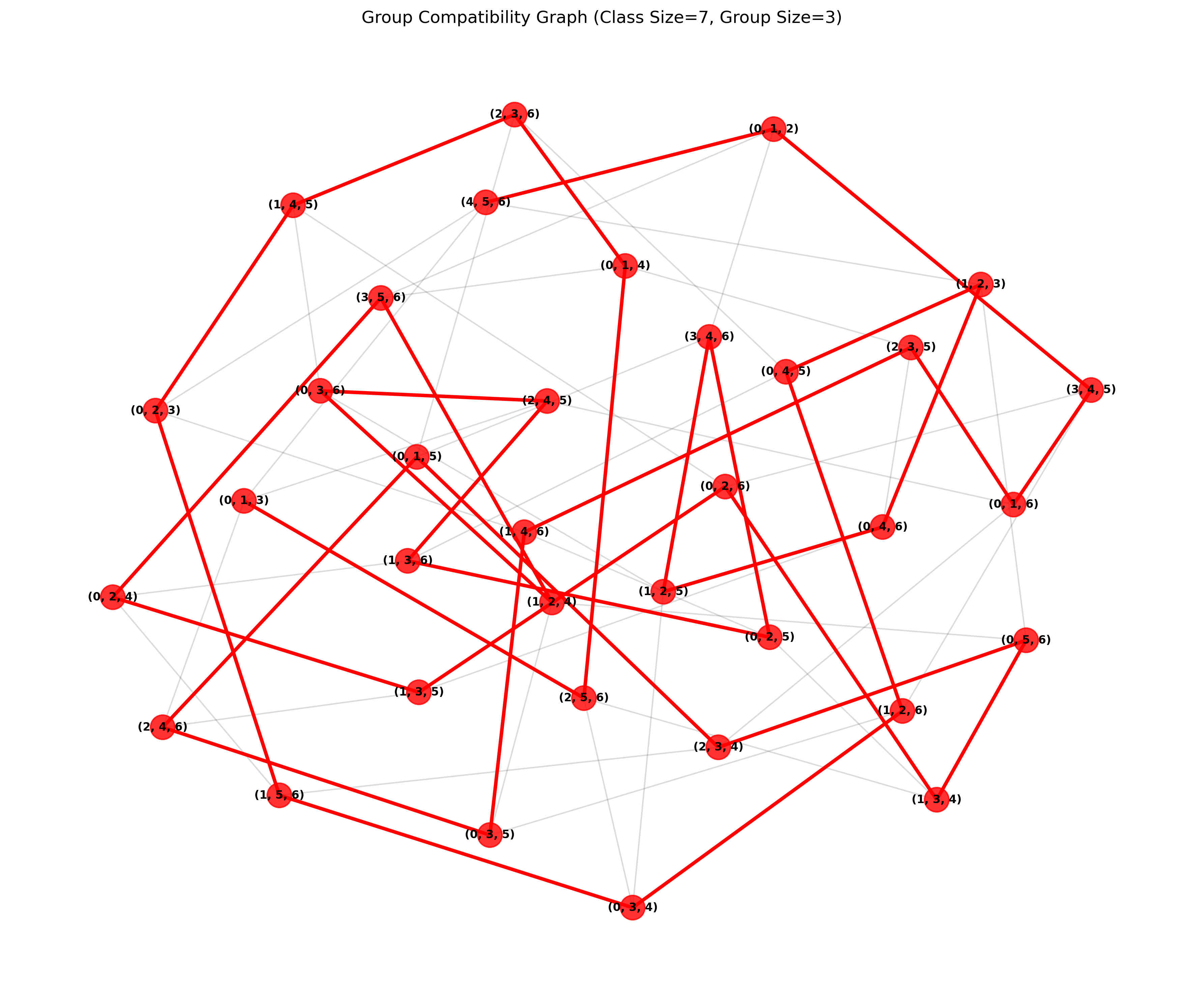
Compatability Graph 7
Click to expand the complete sequence of 35 trios
  1. (0, 1, 5)
  2. (2, 3, 6)
  3. (1, 4, 5)
  4. (0, 3, 6)
  5. (2, 4, 5)
  6. (0, 1, 3)
  7. (2, 4, 6)
  8. (1, 3, 5)
  9. (0, 2, 4)
  10. (1, 5, 6)
  11. (0, 3, 4)
  12. (2, 5, 6)
  13. (0, 1, 4)
  14. (2, 3, 5)
  15. (0, 1, 6)
  16. (2, 3, 4)
  17. (0, 5, 6)
  18. (1, 3, 4)
  19. (0, 2, 6)
  20. (3, 4, 5)
  21. (1, 2, 6)
  22. (0, 3, 5)
  23. (1, 2, 4)
  24. (3, 5, 6)
  25. (0, 1, 2)
  26. (3, 4, 6)
  27. (1, 2, 5)
  28. (0, 4, 6)
  29. (1, 2, 3)
  30. (0, 4, 5)
  31. (1, 3, 6)
  32. (0, 2, 5)
  33. (1, 4, 6)
  34. (0, 2, 3)
  35. (4, 5, 6)

This complete sequence demonstrates that all 35 possible combinations of 3 students from a class of 7 can receive candy while following all the given constraints.

Proving This is the Minimum

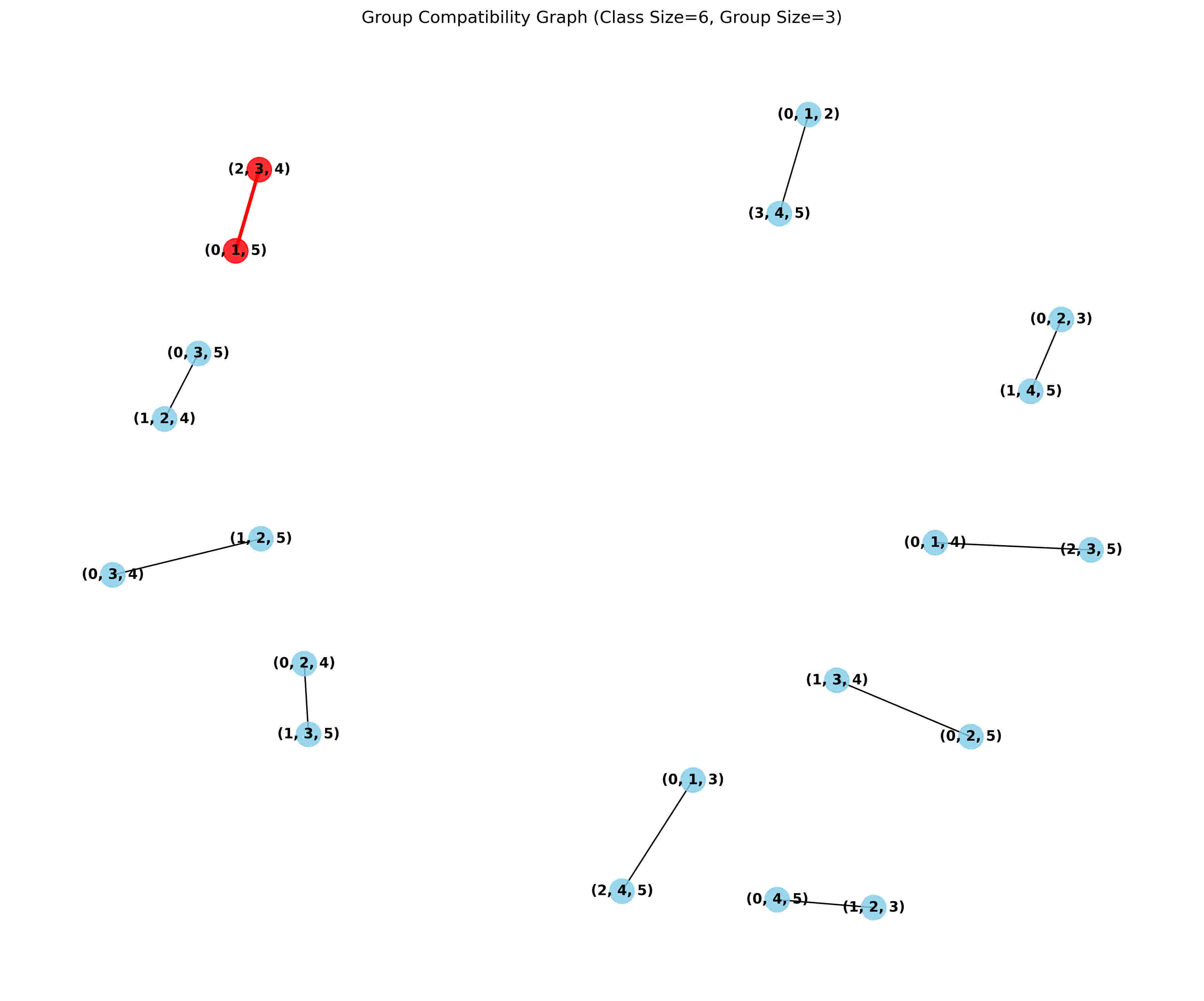
We can confirm that 7 is the smallest possible class size, since the case with 6 students is impossible. With 6 students, there are 20 possible trios, but each trio can only be followed by exactly one other trio (the trio containing the remaining 3 students), creating a severe constraint that makes a complete sequence impossible.

The graph analysis confirms this limitation - with 6 students, the compatibility graph has a very limited structure that cannot support a path visiting all nodes.

Compatability Graph 6

Computational Challenges

The problem was not feasible to brute force due to its complexity. The total number of possible valid orderings is:

(n3)!\binom{n}{3}!

For a class size (nn) of 7, this equates to approximately 35!≈104035! \approx 10^{40} (10 duodecillion) possible orderings. Even with various optimizations, exhaustively searching this space is computationally infeasible.

To overcome this challenge, we used a greedy approach with a heuristic based on the number of valid remaining options. This approach required only hundreds of search attempts to find a complete solution that includes all possible trios.

Conclusion

This puzzle was a bit more straightforward than I expected but still proved to be a fun solve