Barron Wasteland

The Problem

From Dean Ballard comes the perfect puzzle to usher in 2025:

The number 2025 is not prime. As a matter of fact, it’s a perfect square: 2025 = 452.

You cannot make 2025 by adding two distinct primes. To do so, you’d have to add an even prime and an odd prime. The only even prime is 2, but 2025 − 2 = 2023, which is not prime (it’s equal to 7∙172).

But you can make 2025 by adding three distinct primes. For example, 661 + 673 + 691 = 2025.

You can also make 2025 by adding four distinct primes: 2 + 659 + 673 + 691 = 2025.

What is the greatest number of distinct primes that add up to 2025?

My Approach to Finding the Maximum

To find the greatest possible number of distinct primes that sum to n, we developed an algorithmic approach:

Check if n is prime. If so, add it to the list of valid methods
Take 1 and n-1 and add each combination of their valid methods to n's valids methods if there are no repeated values
Repeat for 2 and n-2, 3 and n-3, etc, until you reach n/2

This method uses the solutions from smaller numbers to determine the paths to get to larger numbers.

While comprehensive, it also expands geometrically. Here we can see how the number of valid paths to each value grows over time:

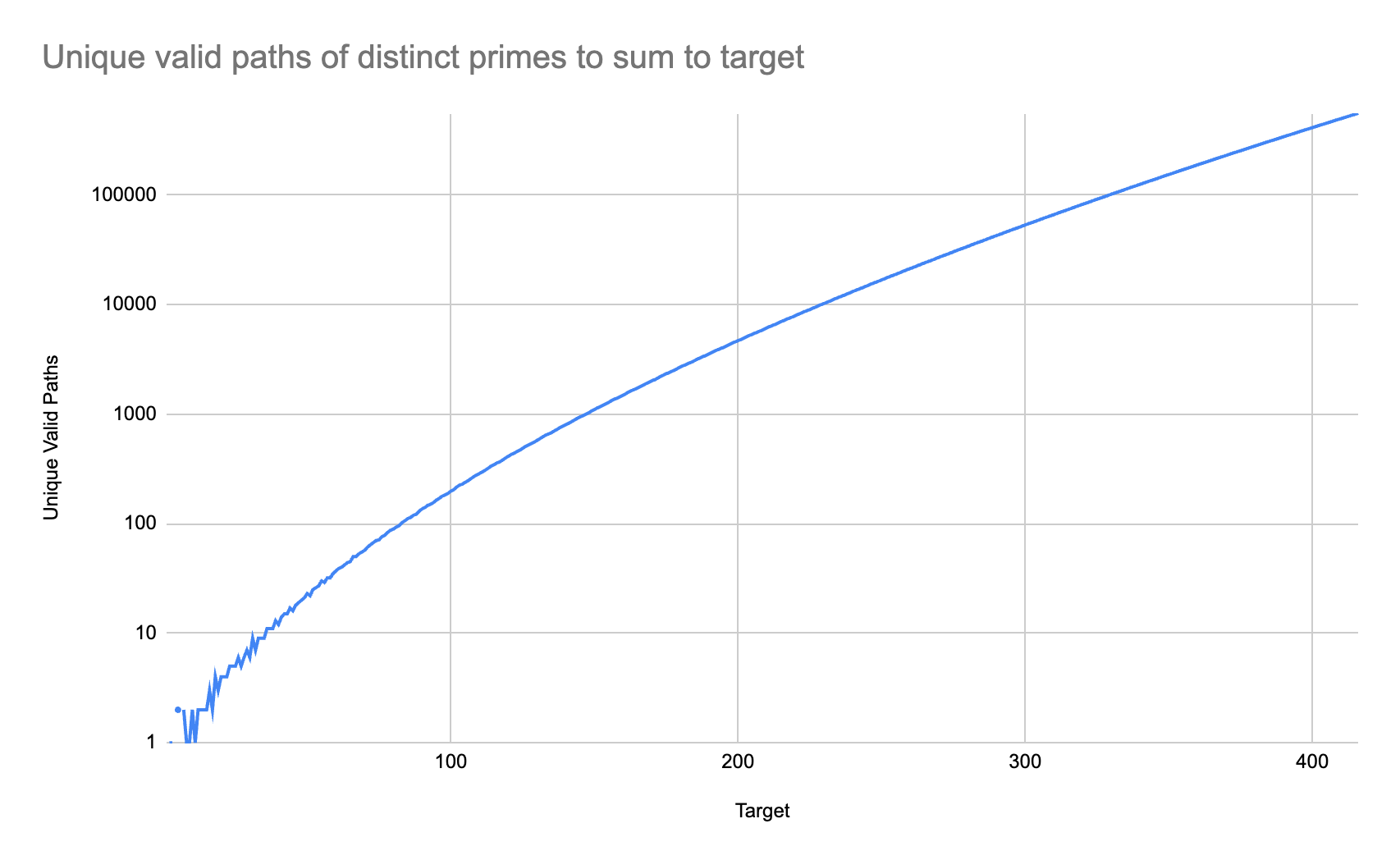
Computational Challenges

The problem quickly becomes computationally intensive due to its geometric growth. Even with several optimizations including:

Multiprocessing
Local database caching
Efficient prime number generation

This helped us compute solutions up to 400 on a laptop after several days of computation. I suspect there must be a more efficient way, although I could not come up with it.

I have made the code used for this available here in case others would like to view or improve it. The spreadsheet of number of valid methods is available here

Conclusion

While we couldn't directly solve for 2025, my investigation led us to sequence A261153 in the OEIS which appears to be very similar. Overall, this puzzle was fun and led to an interesting problem solving experience and I am interested to see how others may have optimized their solutions