DATA-DRIVEN ARMAGEDDON CHESS BIDDING
The Problem
Armageddon is a decisive tiebreak format where players bid on how much time they need to win with White. The player who bids the lowest time gets White, while the other player gets Black with draw odds (a draw counts as a win for Black).
The question is: how much should you bet?
I am attempting to take a more data-driven approach by analyzing average centipawn loss (ACPL) across different time controls and rating levels. By understanding how player accuracy degrades at various time controls, you can better assess the true value of time in Armageddon scenarios.
Note: This project is a work in progress. I'm continuing to refine the analysis and gather more data, but the initial findings are interesting enough to share.
My Approach
All game data is sourced from the Lichess Open Database, which provides millions of analyzed games with Stockfish evaluations. The current analysis is based on 21 million games, with more data being processed as we speak.
The analyzer processes PGN files with evaluation data and outputs metrics for each player including:
- Average centipawn loss (ACPL) during middlegame
- Inaccuracies, mistakes, and blunders
- Time control and rating information
I only analyze the midgame since openings are often rote and endgames can often inflate the ACPL since it can often include a lot of moves with marginal impact
Games are categorized by time controls and rating buckets (200-point intervals).
The full code and analysis is available on GitHub.
Key Findings
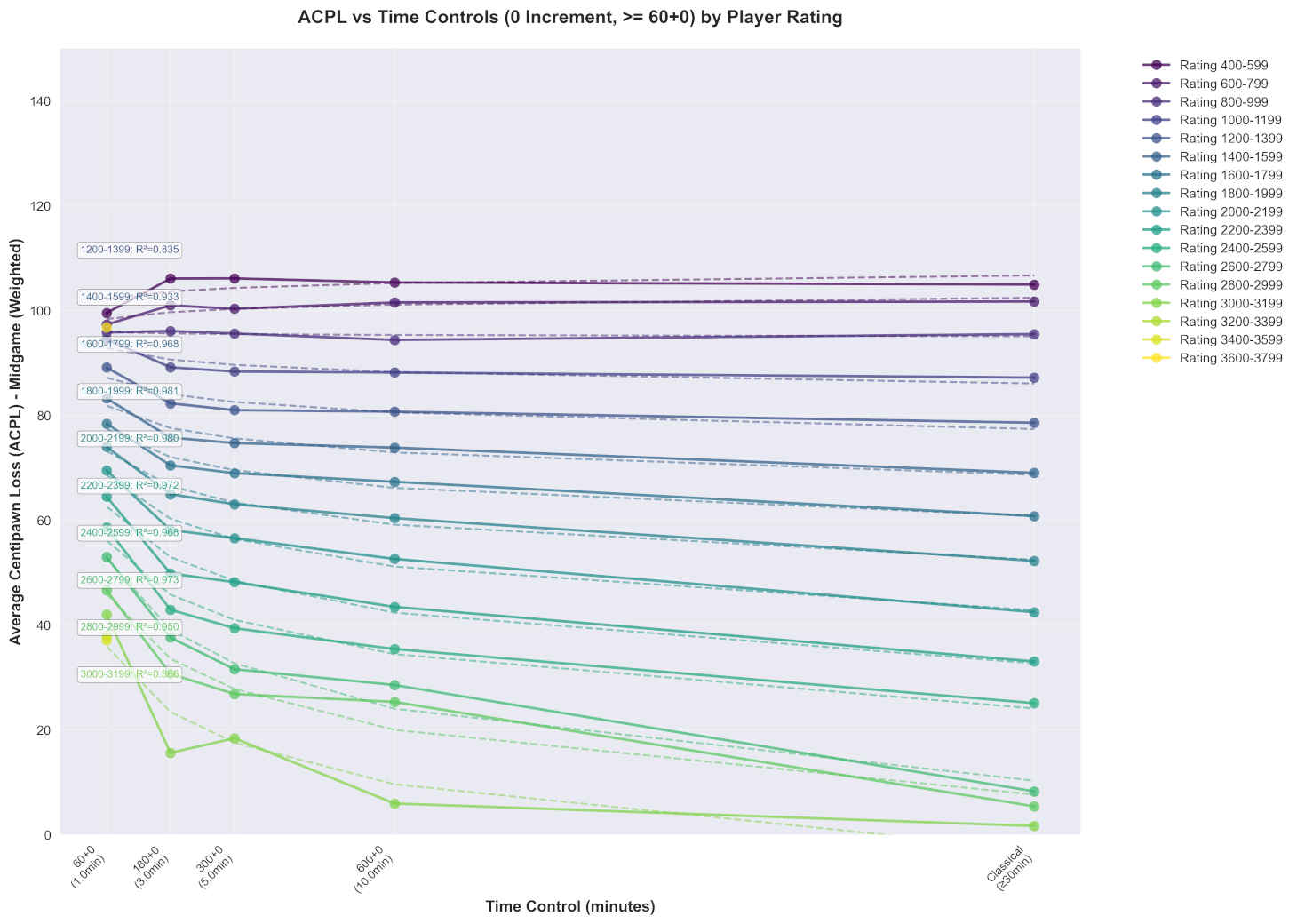
Time pressure significantly impacts accuracy: ACPL increases as time controls get shorter, with the effect more pronounced at lower rating levels.
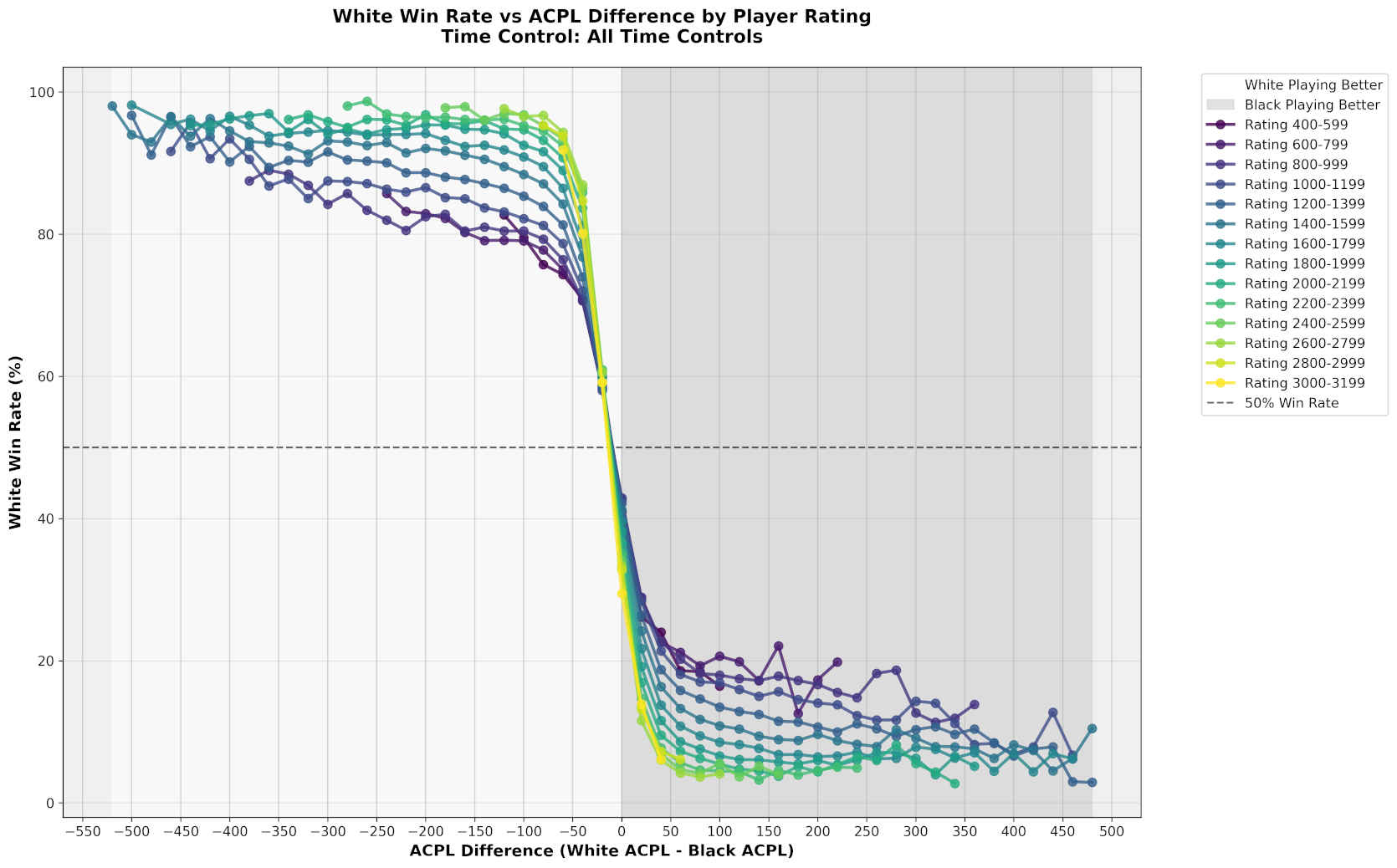
ACPL strongly predicts outcomes: ~50 ACPL advantage correlates with 85-95% win rate across all rating levels (r ≈ -0.95).
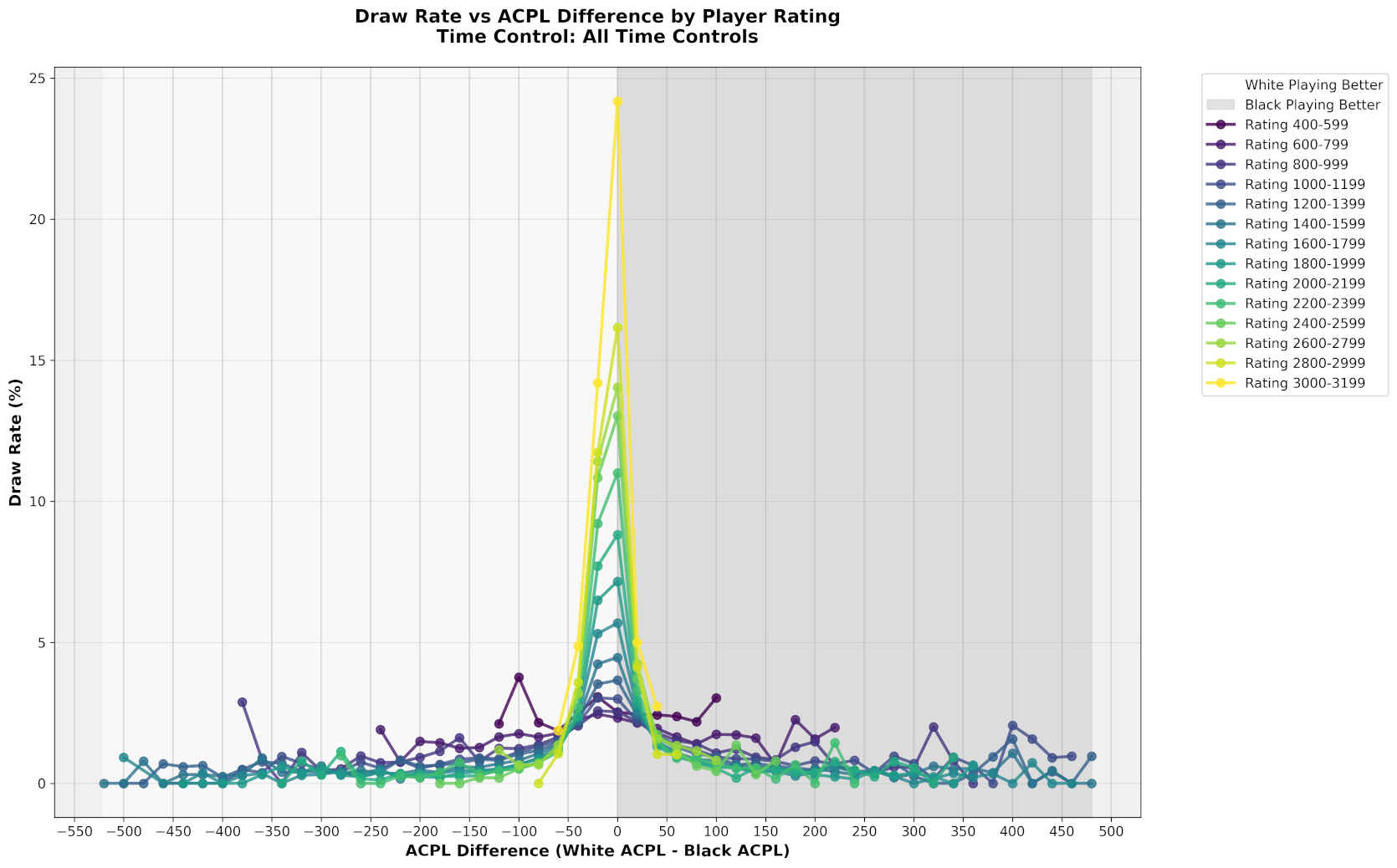
Draw rates increase with skill and equal play: Higher-rated players (2200+) draw 15-20% of games when ACPL is equal, compared to <5% for lower-rated players.
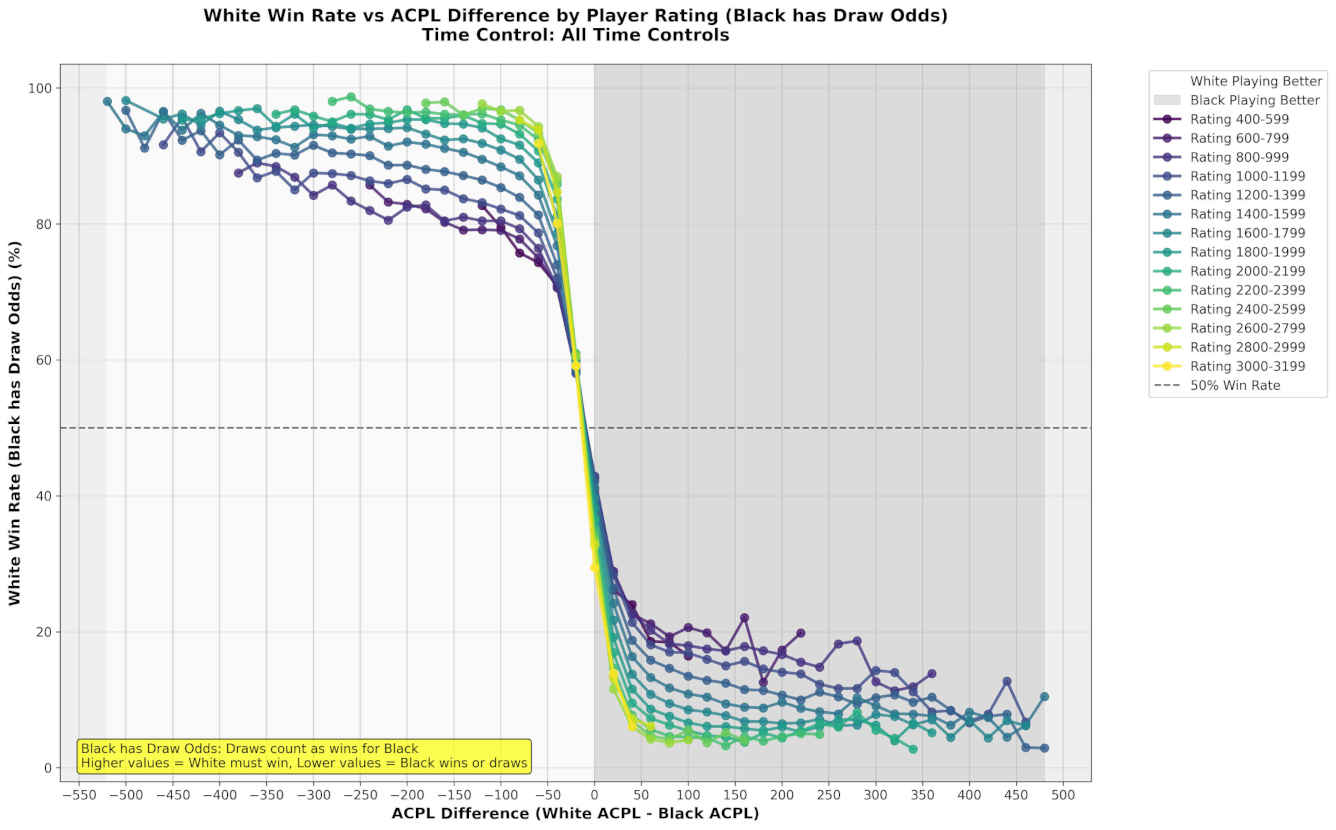
Draw odds are valuable: When Black has draw odds, White needs significantly better play to achieve 50% winning probability.
What's Next
The data provides insights into how time pressure affects play quality, but there's more work to be done. I'm hoping to have a recursive framework similar to SimonM's approach, with an additional step that maps time controls to expected ACPL loss for improved accuracy.
Check out the full analysis on GitHub if you want to explore the data yourself or contribute to the project.