What is the Riddler?

The Riddler is a weekly math, logic and probability problem hosted by fivethirtyeight. The website usually posts data-driven politics, sports and culture blog and predictions.

The Riddler Logo

If my solution is extendable, interactive or generalizable then I'll usually blog about it. I've also created and submitted some problems that have been published on the column.

Submitted Problems

A Pizza Sauce Problem

This problem is about filling a pizza evenly with sauce.

You work for Puzzling Pizza, a company committed to making the best and most consistent pizzas in town. As the shop's resident mathematician, your boss has asked you to design a product similar to one they saw online:

Link to video

They've already purchased the equipment but need to know the exact path and flow rate the sauce-dispensing arm should use to fill a 12-inch circular pizza with sauce as fully and evenly as possible.

This problem was unique in that I not only created the problem but also wrote the solution and provided the diagrams.

Pizza sauce dispensing path

The solution can be found here

Barron Squares

This is a mathematical object. It is a square matrix such that each row's leftmost element times its rightmost element will equal the two inner numbers (in the example below, the top row has 6*7 = 42).

Similarly, each column's uppermost element times the column's lowermost element equals the middle digits (in the example, the right column is 7*8 = 56), as read top to bottom.

4x4 Barron Square

This was then expanded on to be an 8x8 with two digit rows/columns being multiplied to get four digit products

8x8 Barron Square

We ended up finding all 1444 4x4 Barrons Squares, several hundred 8x8 and even a few 16x16 Barron Squares. This was featured as a Riddler Express for FiveThirtyEight.

Problem Solutions

Putting Sharp Objects into Round Ones

This problem was about creating triangles in a unit circle and determining if the circle's center was enclosed.

"Choose three points on a circle at random and connect them to form a triangle. What is the probability that the center of the circle is contained in that triangle?"

This led to the following visualization:

2d Simulation

3D Case

Choose four points at random (independently and uniformly distributed) on the surface of a sphere. What is the probability that the tetrahedron defined by those four points contains the center of the sphere?

3d Simulation

The probability that the shapes would enclose the center resulted in surprisingly nice 25% and 12.5%.

Gerrymandering

Below is a rough approximation of Colorado's voter preferences, based on county-level results from the 2012 presidential election, in a 14-by-10 grid. Colorado has seven districts, so each would have 20 voters in this model. What is the most districts that the Red Party could win if you get to draw the districts with the same rules as above? What about the Blue Party? (Assume ties within a district are considered wins for the party of your choice.)

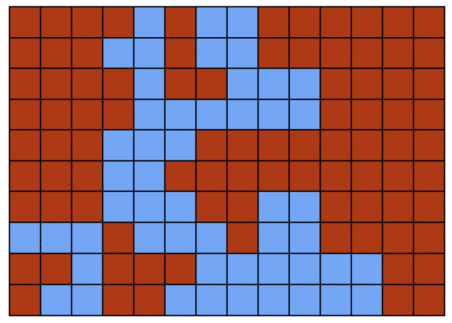
Colorado's voter preferences

We used a randomized search that would try to slightly move districts, check continuity and then check the voting results. The method resulted in uniquely shaped maps that optimized each side's winningness.

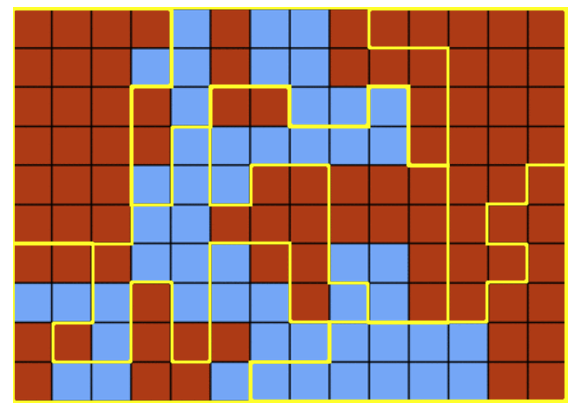
Optimized districts for Blue Party

Districts move their boundaries each iteration

FiveThirtyEight's The Riddler